Vishrut Kinikar
Are dimensions a mere product of the mind? This question has been been endlessly debated in various philosophical traditions and has entered the domain of science in the past few centuries. This mere question, and other questions regarding the existence of dimensions, have been the driving force behind a plethora of philosophical traditions and scientific theories. The Indian philosophical tradition lists dik (space) and kaal (time) to be the extant dimensions of the universe, and further goes on to state that these dimensions are a mere product of the mind. However there is, still to this day, great discord between physicists over this question and although this question may have no definite answer, the alternate question of whether higher dimensions can be visualized has a beautiful edifice of research behind it, and one such beautiful piece of research is the research behind Graham’s number.
Graham’s number is an immense number and a hypercube possessing this specific amount of dimensions is said to be the upper bound by which a certain configuration of a two-dimensional quadrilateral plane cannot be avoided. The problem whose solution’s upper bound is the Graham’s number had for a substantial time period, afflicted the minds of the finest mathematicians, but was finally solved in 1971 by Ronald Graham, in whose honor this immense number was christened “Graham’s Number”.
The special configuration described previously exists on a two-dimensional plane. If a square is drawn on a flat plane, it will have four vertices and four edges. Two diagonals will then be added, intersecting the vertices as such:
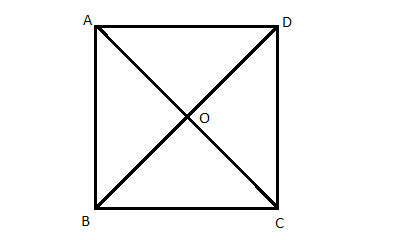
This plane figure now has six edges. Each of these edges can be colored red or blue and various configurations of colored edges can be generated. For example, one edge can be colored blue and the rest red, or it can be the other way around with one edge red and the rest of the edges blue. Or two can be red and four can be blue (or two can blue or four can be red), or half of the edges can be red and half of them can be blue. Such configurations of colors of the edges can be generated, however, there exists a special configuration which is to be avoided.
The special configuration is the configuration where all edges are colored either blue or all edges are red. The goal is to find in how many dimensions this configuration cannot be avoided. In two dimensions, it can be obviously avoided as the edges can be colored with both blue and red. In three dimensions it can also be avoided. In a three-dimensional cube, there are eight vertices and 28 possible line segments that can be drawn which will connect the vertices. These can be colored blue and red without having a two-dimensional cross-section with all line segments having the same color. If the cube is extended to four dimensions, we can have a hypercube. A cube in four dimensions is known as a tesseract and after coloring all of the possible line segments which are possible, it can be seen that the special configuration (a two-dimensional face with all edges colored in the same color) can be avoided. It can be avoided until all dimensions until 13 dimensions. In 13 dimensions, it is possibly unavoidable but it is not known with certainty due to increased difficulty of calculation with higher-dimensional figures. This is why 13 is the lower bound on the answer to this problem. Previously, the lower bound to this problem was thought to be 11 dimensions, but after recent breakthroughs, the lower bound has been increased to 13 dimensions. The upper bound on the solution is Graham’s number. Graham’s number being the upper bound to this problems means that by Graham’s number amount of dimensions, the special configuration is unavoidable no matter how the line segments in the hypercube are colored. How large is Graham’s number, though? Graham’s number has a magnitude of such a large scale that it dwarfs even integers of the order of a googolplex or a googolplexian. Graham’s number has magnitude so great that it cannot be expressed using powers. Instead it has to be written using a special notation known as Knuth’s up-arrow notation. Invented in 1976, this 47-year old system has a beautiful algorithm which enables it to exponentiate numbers on a scale unachievable with simple arithmetic operations.
Knuth’s up-arrow makes use of upward-pointing arrows, and the amount of arrows drastically alters the value of the expression in which it is being utilized. For example, the expression 3↑3 is equal to 33 = 27. However, if the given expression is 3↑↑3, the algorithm must be applied. The algorithm is that if a↑nb, with b being an integer and n being the amount of arrows, the expression is equal to a written down b times which n-1 arrows between each pairs of a’s. Thus, for 3↑↑3, 3 is written down three times with 2-1 = 1 between each pair of 3’s. The simplified form of this expression is thus 3↑3↑3, which is then equal to 3^(33) = 327, which is approximately equal to 7.6 trillion. From these two examples alone, the efficiency behind this notation an be seen. Just by adding one arrow between 3 and, the value of the expression leapt from 27 to 7.6 trillion, which makes it a wonderful system for exponentiation on an immense scale. An additional example is as follows: suppose the expression 3↑↑↑3 is given. Following the algorithm, there are three 3’s with 3-1 = 2 arrows between each pair of 3’s. Expressed mathematically, this is as follows: 3↑↑3↑↑3. The expression can be simplified as follows: 3↑↑(3↑3↑3) = 3↑↑(7.6 x 1012). The number that has been reached is so massive that it cannot be written using only single arrows in between 3’s. Using the algorithm, 3↑↑(7.6 x 1012) is equal to 7.6 trillion 3’s with an arrow between each 3, which is 3^3^3^3^3^3^3^3… with a total of 7.6 trillion 3’s. From the given examples, it is evident that adding more arrows increase the value of the number on an ineffable scale.
In order to fathom the magnitude of Graham’s number, one must first start with a quantity equal to 3↑↑↑↑3. The sheer magnitude of this number is so immense that even comprehending it is beyond the realm of human cognition. This number will be assigned the name G1. This number has been taken is to build a tower of numbers. The next member of this tower would be two 3’s with 3↑↑↑↑3 arrows between them. This number will be assigned the name G2. The next number will be G3, equivalent to two 3’s with G2 arrows between them. The next number is G4, equivalent to two 3’s with G3 arrows in between. The next number is G5, equivalent to two 3’s with G4 arrows between them, and the pattern continues. As this tower of large numbers is continuously built up, one of the number in the tower is G64, which you may have figured out already, is equivalent to two 3’s with G63 arrows between them. This is the value of Graham’s number. Graham’s has a magnitude so enormous that its value cannot even be written physically in terms of Knuth’s up-arrows. Imagine having two write down two 3’s with G63 arrows between them on paper! There would not be enough paper in the universe nor years in the human lifetime to accomplish such a feat. In other words, Graham’s number can only be conceived using Knuth’s up-arrow notation but never be written down in terms of it. It becomes very clear from this that the magnitude of Graham’s number is beyond astronomical. After getting to comprehend the magnitude of Graham’s number, one may wonder what digits are present in the decimal notation of Graham’s number. Mathematicians, to this day, have been unable to calculate the amount of digits in Graham’s number. They not even been able to figure out it’s first digit. However, mathematicians have been able to unearth a few interesting facts about Graham’s number’s decimal notation. They have found that Graham’s number has 7 as its final digit and that Graham’s number is divisible by 3 (this also means that the sum of the digits of Graham’s number are equivalent to a number divisible by 3). Unfortunately, these facts do not help mathematicians in figuring out the decimal notation of this massive number, and maybe the value may never be figured out, but the mere discovery of Graham’s number has given the scientific community more confidence in mathematically analyzing the possibility of higher dimensions. Graham’s number alone serves as a step in the direction towards being able to mathematically formulate a colossal amount of macro-dimensions, and will lead to more discoveries which may one day lead to a kind of mathematical toolkit. This toolkit of mathematical formulations in higher dimensions may very well be utilized to create more efficient theorizations of higher dimensions in the upcoming future.